Recurrence Quantification Analysis

This vignette discusses how to conduct a large variety of recurrence-based time series analyses using R-package casnet. It is not the only R package that can run recurrence analyses, the closest alternative in R to casnet is probably package crqa. It has a great tutorial paper by [@coco2014]). Several other packages have dedicated functions, e.g. package nonlinearTseries has a function RQA. There are also many options outside of the R framework, see the Recurrence Plot webpage for a comprehensive list of software.

There are 3 ways to run Recurrence Quantification Analyses in casnet:

Using functions rp, rp_measures and rp_plot. These functions use a thresholded distance matrix known as a recurrence plot to calculate RQA measures. Use these functions if your time series length is around 2000 data points or less.
Using function rqa_par, which does not construct a distance matrix, but processes matrix diagonals in parallel. The function is very fast and can handle very large time series.
Using function rqa_cl which will run Norbert Marwan’s commandline Recurrence Plots. You can run this if your OS allows execution of 32 bit command line executable.

The following examples will demonstrate the basic use of the native casnet functions based on the rqa_par and rp families of functions, see the paragraph An R interface to Marwan’s commandline recurrence plots to learn about using rqa_cl() and An R interface to Marwan’s commandline recurrence plots.

To learn more about the different types of Recurrence Quantification Analysis that can be conducted in casnet please see the chapters on RQA in the Complex Systems Approach book for more details:

RQA based on a matrix: `rp()`

Unordered categorical data

emDim   <- 1
emLag   <- 1
emRad   <- 0
theiler <- 0 # Do not include the diagonal

Continuous data

We’ll use the examples used in the manual of the PyRQA library for Python. This is convenient, the parameters emDim, emLag and emRad are already given (see the CSA book for examples on how to estimate them with casnet) and it allows for a comparison of the output.

# PyRQA example data
data_points <- as.numeric(c(0.1, 0.5, 1.3, 0.7, 0.8, 1.4, 1.6, 1.2, 0.4, 1.1, 0.8, 0.2, 1.3))

plot(ts(data_points), type = "b")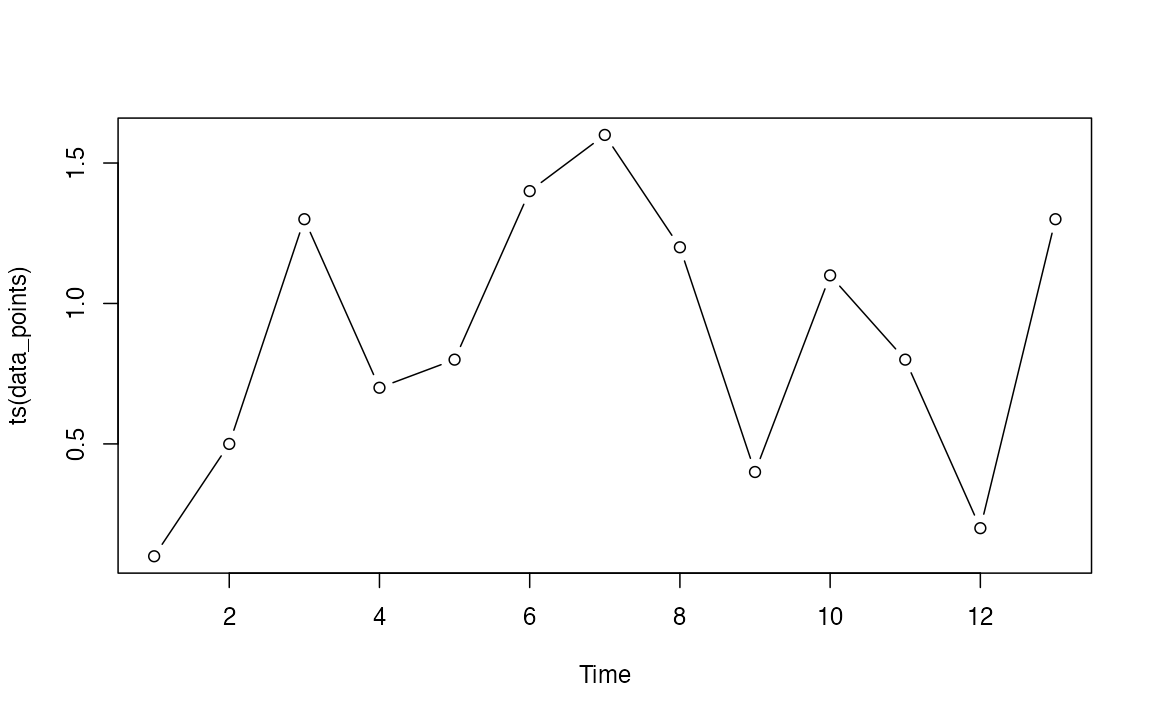

First, we create a distance matrix based on the (delay embedded) time series and decide on a threshold criterion to turn it into a recurrence matrix of 0s and 1s. We already have a radius given in the PyRQA example, using a convenient graphical tool for visual inspection of the relationship between different thresholds values and the resulting recurrence rate (RR), we can check what this radius will yield.

library(casnet)

emDim   <- 2
emLag   <- 2
emRad   <- 0.65

RM <- rp(y1 = data_points, emDim = emDim, emLag = emLag)
rp_plot(RM, plotDimensions = TRUE, drawGrid = TRUE)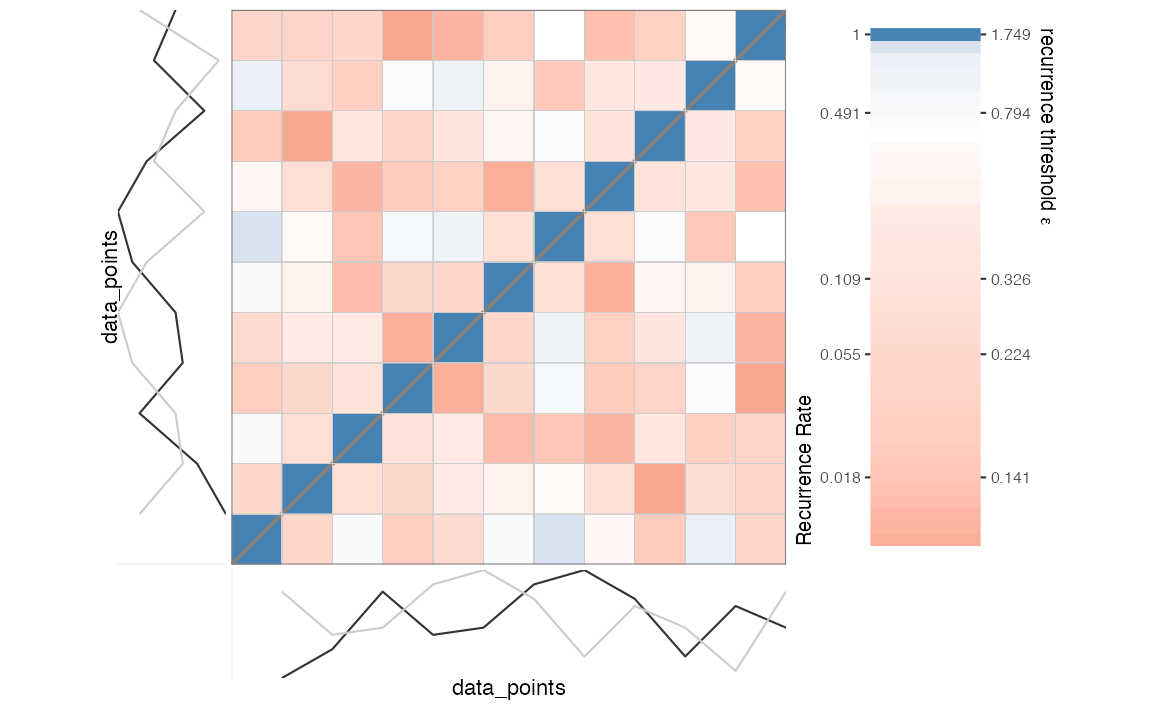

The code below applies the threshold emRad to the distance matrix, which generates a sparse matrix (class dgcMatrix, see package [Matrix]).

(RM <- rp(y1 = data_points, emDim = emDim, emLag = emLag, emRad = emRad))

> 11 x 11 sparse Matrix of class "dgCMatrix"
>                            
>  [1,] . . . 1 . . . . 1 . .
>  [2,] . . . . . . . . 1 . .
>  [3,] . . . . . 1 1 1 . 1 .
>  [4,] 1 . . . 1 . . 1 . . 1
>  [5,] . . . 1 . . . 1 . . 1
>  [6,] . . 1 . . . . 1 . . 1
>  [7,] . . 1 . . . . . . 1 .
>  [8,] . . 1 1 1 1 . . . . 1
>  [9,] 1 1 . . . . . . . . 1
> [10,] . . 1 . . . 1 . . . .
> [11,] . . . 1 1 1 . 1 1 . .

The relevant analysis parameters, including the embedded series, are stored as attributes of the matrix object.

attributes(RM)

> $i
>  [1]  3  8  8  5  6  7  9  0  4  7 10  3  7 10  2  7 10  2  9  2  3  4  5 10  0
> [26]  1 10  2  6  3  4  5  7  8
> 
> $p
>  [1]  0  2  3  7 11 14 17 19 24 27 29 34
> 
> $Dim
> [1] 11 11
> 
> $Dimnames
> $Dimnames[[1]]
> NULL
> 
> $Dimnames[[2]]
> NULL
> 
> 
> $x
>  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
> 
> $factors
> list()
> 
> $class
> [1] "dgCMatrix"
> attr(,"package")
> [1] "Matrix"
> 
> $method
> [1] "Euclidean"
> 
> $call
> proxy::dist(x = et1, y = et2, method = method, diag = TRUE)
> 
> $AUTO
> [1] TRUE
> 
> $emRad
> [1] 0.65
> 
> $NAij
> [1] NA
> 
> $theiler
> [1] 1
> 
> $emDims1
>       tau.0 tau.1
>  [1,]   0.1   1.3
>  [2,]   0.5   0.7
>  [3,]   1.3   0.8
>  [4,]   0.7   1.4
>  [5,]   0.8   1.6
>  [6,]   1.4   1.2
>  [7,]   1.6   0.4
>  [8,]   1.2   1.1
>  [9,]   0.4   0.8
> [10,]   1.1   0.2
> [11,]   0.8   1.3
> attr(,"embedding.dims")
> [1] 2
> attr(,"embedding.lag")
> [1] 2
> attr(,"embedding.time")
> [1] 2
> attr(,"variable.y")
> [1] "data_points"
> 
> $emDims2
>       tau.0 tau.1
>  [1,]   0.1   1.3
>  [2,]   0.5   0.7
>  [3,]   1.3   0.8
>  [4,]   0.7   1.4
>  [5,]   0.8   1.6
>  [6,]   1.4   1.2
>  [7,]   1.6   0.4
>  [8,]   1.2   1.1
>  [9,]   0.4   0.8
> [10,]   1.1   0.2
> [11,]   0.8   1.3
> attr(,"embedding.dims")
> [1] 2
> attr(,"embedding.lag")
> [1] 2
> attr(,"embedding.time")
> [1] 2
> attr(,"variable.y")
> [1] "y2"
> 
> $emDims1.name
> [1] "data_points"
> 
> $emDims2.name
> [1] "y2"
> 
> $embedded
> [1] TRUE
> 
> $emLag
> [1] 2
> 
> $emDim
> [1] 2
> 
> $measures
> [1] NA
> 
> $weighted
> [1] FALSE
> 
> $weightedBy
> [1] "si"
> 
> $chromatic
> [1] FALSE
> 
> $chromaNames
> [1] NA
> 
> $chromaDims
> [1] NA

It is custom to represent the recurrence matrix as a plot with coordinate (1,1) in the left lower corner.

rp_plot(RM, plotDimensions = TRUE, drawGrid = TRUE)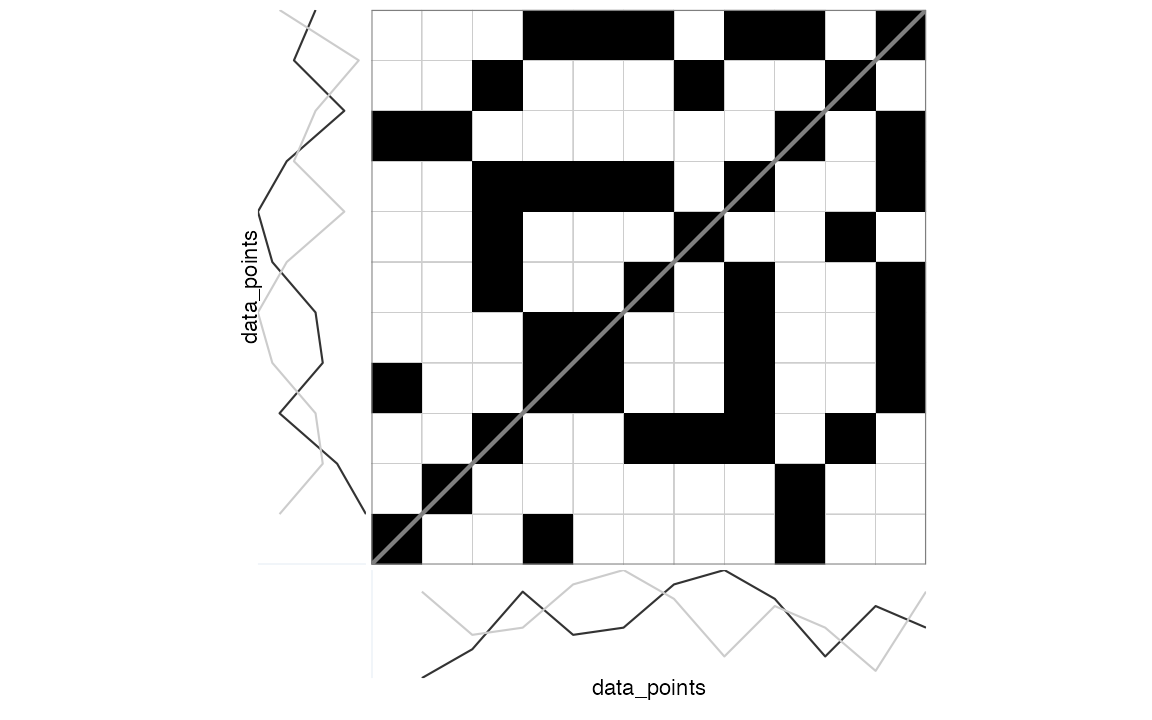

Because this analysis concerns Auto-RQA, the diagonal is usually excluded from the calculations of RQA measures. This can be achieved by setting the theiler parameter to 1. This is in fact the default behavior in casnet if the theiler argument is NA and the recurrence matrix is detected to be symmetrical.

# Current value of theiler
attributes(RM)$theiler

> [1] 1

# Values on the diagonal
Matrix::diag(RM)

>  [1] 0 0 0 0 0 0 0 0 0 0 0

# To explicitly include the diagonal in calculations set theiler to 0
(RM <- rp(y1 = data_points, emDim = emDim, emLag = emLag, emRad = emRad, theiler = 0))

> 11 x 11 sparse Matrix of class "dgCMatrix"
>                            
>  [1,] 1 . . 1 . . . . 1 . .
>  [2,] . 1 . . . . . . 1 . .
>  [3,] . . 1 . . 1 1 1 . 1 .
>  [4,] 1 . . 1 1 . . 1 . . 1
>  [5,] . . . 1 1 . . 1 . . 1
>  [6,] . . 1 . . 1 . 1 . . 1
>  [7,] . . 1 . . . 1 . . 1 .
>  [8,] . . 1 1 1 1 . 1 . . 1
>  [9,] 1 1 . . . . . . 1 . 1
> [10,] . . 1 . . . 1 . . 1 .
> [11,] . . . 1 1 1 . 1 1 . 1

attributes(RM)$theiler

> NULL

In casnet the theiler correction will affect all calculations. This is different from, for example, PyRQA where it only affects the recurrence rate and measures based on diagonal line structures. Below are the results reported in the online PyRQA manual, with the diagonal included:

RQA Result:
===========

Minimum diagonal line length (L_min): 2
Minimum vertical line length (V_min): 2
Minimum white vertical line length (W_min): 2

Recurrence rate (RR): 0.371901
Determinism (DET): 0.411765
Average diagonal line length (L): 2.333333
Longest diagonal line length (L_max): 3
Divergence (DIV): 0.333333
Entropy diagonal lines (L_entr): 0.636514
Laminarity (LAM): 0.400000
Trapping time (TT): 2.571429
Longest vertical line length (V_max): 4
Entropy vertical lines (V_entr): 0.955700
Average white vertical line length (W): 2.538462
Longest white vertical line length (W_max): 6
Longest white vertical line length inverse (W_div): 0.166667
Entropy white vertical lines (W_entr): 0.839796

Ratio determinism / recurrence rate (DET/RR): 1.107190
Ratio laminarity / determinism (LAM/DET): 0.971429

The same for casnet:

# Including diagonal
RM <- rp(y1 = data_points, emDim = emDim, emLag = emLag, emRad = emRad, theiler = 0)
out_rqa <- rp_measures(RM, silent = FALSE)

> 
> ~~~o~~o~~casnet~~o~~o~~~
>  Global Measures
>   Global Max.points N.points    RR Singular Divergence Repetitiveness
> 1 Matrix        110       45 0.409       20      0.333              2
> 
> 
>  Line-based Measures
>        Lines N.lines N.points Measure  Rate Mean Max.   ENT ENT_rel   CoV
> 1   Diagonal       6       14     DET 0.311 2.33    3 0.637   0.265 0.221
> 2   Vertical       5       14   V LAM 0.311 2.80    4 1.055   0.440 0.299
> 3 Horizontal       5       14   H LAM 0.311 2.80    4 1.055   0.440 0.299
> 4  V+H Total      10       28 V+H LAM 0.311 2.80    4 1.055   0.440 0.282
> 
> ~~~o~~o~~casnet~~o~~o~~~

Below is a comparison of the output from casnet::rp() and PyRQA. Note that PyRQA includes the main diagonal for RR and measures based on vertical (and horizontal) lines.

Measure	rp (theiler = 0)	rp (theiler = 1)	PyRQA (theiler_corrector = 1)	PyRQA Diagonal included?

RR	0.409091	0.309091	0.371901	Yes
DET	0.311111	0.411765	0.411765	No
MAX_dl	3.000000	3.000000	3.000000	No
MEAN_dl	2.333333	2.333333	2.333333	No
ENT_dl	0.636514	0.636514	0.636514	No
LAM	0.311111	0.411765	0.400000	Yes
MAX_vl	4.000000	4.000000	4.000000	Yes
MEAN_vl	2.800000	2.800000	2.571429	Yes
ENT_vl	1.054920	1.054920	0.955700	Yes

RQA based on massively parallel processing: `rqa_par()`

PyRQA was developed to perform RQA on very long time series, without overloading memory and inflating the computing time to a degree that is unmanageable in a regular workflow. It is not recommended to use matrix based functions like casnet::rp_measures() on time series larger than 5,000 data points, instead, casnet::rqa_par() can be used, which implements some of the methods used in PyRQA. Specifically, the memory management by limiting the precision (package [float]) and using bit compression (package [float]), as well as by computing RQA measures in a massively parallel way (package [parallel]). Compared to casnet::rqa_par(),PyRQA is still faster, but this difference becomes noticeable for very large time series (>100,000).

noise <- casnet::noise_powerlaw(N=10000, seed = 1234)
plot(ts(noise),type = "l")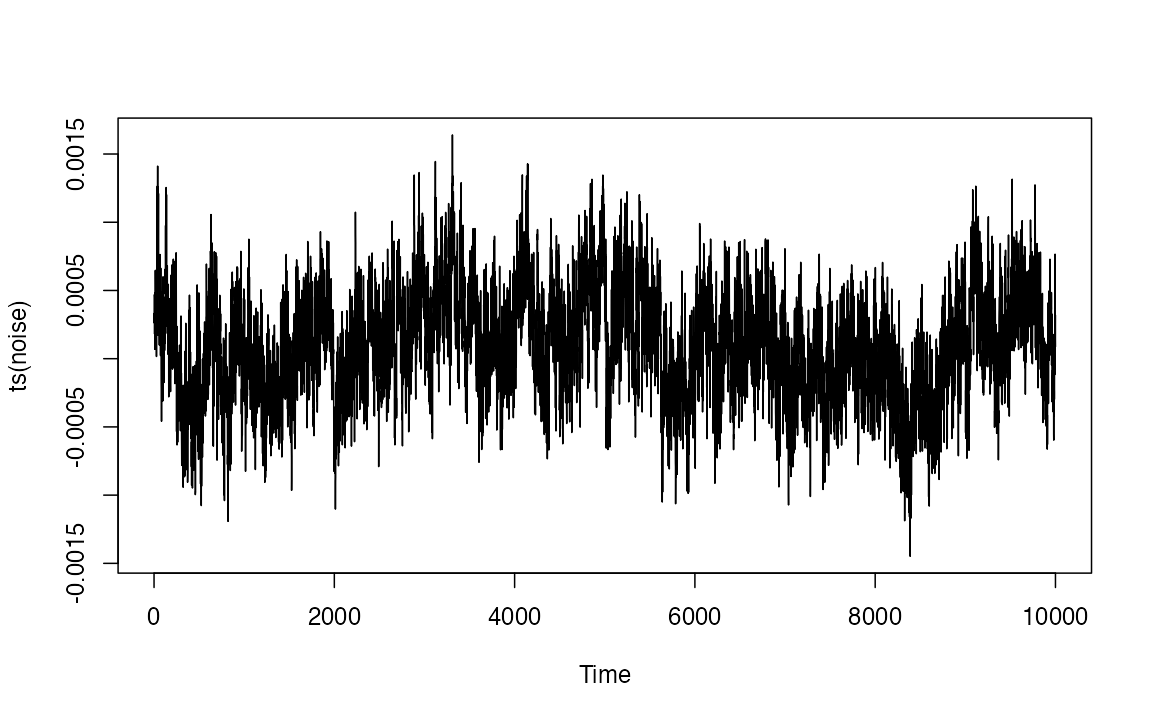

#est_radius_rqa(ts_embed(noise, emDim = emDim, emLag = emLag), noise, AUTO = TRUE)

RQA Result:
===========

Minimum diagonal line length (L_min): 2
Minimum vertical line length (V_min): 2
Minimum white vertical line length (W_min): 2

Recurrence rate (RR): 0.049585
Determinism (DET): 0.230880
Average diagonal line length (L): 2.149236
Longest diagonal line length (L_max): 7
Divergence (DIV): 0.142857
Entropy diagonal lines (L_entr): 0.443727
Laminarity (LAM): 0.374149
Trapping time (TT): 2.305511
Longest vertical line length (V_max): 8
Entropy vertical lines (V_entr): 0.709903
Average white vertical line length (W): 28.154700
Longest white vertical line length (W_max): 9079
Longest white vertical line length inverse (W_div): 0.000110
Entropy white vertical lines (W_entr): 3.909756

Ratio determinism / recurrence rate (DET/RR): 4.656240
Ratio laminarity / determinism (LAM/DET): 1.620535

# Including diagonal
# emRad <- est_radius(rp(noise,emDim = emDim, emLag = emLag))
emLag <- 100
emDim <- 2
emRad <- .00018
out_rqa_par <-  casnet::rqa_par(y1 = noise, AUTO = TRUE, emDim = emDim, emLag = emLag, emRad = emRad, silent = FALSE, theiler = 0)

> 
> ~~~o~~o~~casnet~~o~~o~~~
>  Global Measures
>   Global Max.points N.points     RR Singular Divergence Repetitiveness
> 1 Matrix    9.8e+07  4859832 0.0496  3730180   0.000101           3.22
> 
> 
>  Line-based Measures
>        Lines N.lines N.points Measure  Rate Mean Max.   ENT ENT_rel   CoV
> 1   Diagonal  521001  1129652     DET 0.232 2.17 9900 0.444  0.0482 6.327
> 2   Vertical  788676  1818301   V LAM 0.374 2.31    8 0.710  0.0772 0.269
> 3 Horizontal  788676  1818301   H LAM 0.374 2.31    8 0.710  0.0772 0.269
> 4  V+H Total 1577352  3636602 V+H LAM 0.374 2.31    8 0.710  0.0772 0.269
> 
> ~~~o~~o~~casnet~~o~~o~~~

Measure	crqa_par (theiler = 0)	crqa_par (theiler = 1)	PyRQA (theiler_corrector = 1)	PyRQA Diagonal included?

RR	0.049585	0.049489	0.049585	Yes
DET	0.232447	0.230880	0.230880	No
MAX_dl	9900.000000	7.000000	7.000000	No
MEAN_dl	2.168234	2.149236	2.149236	No
ENT_dl	0.443753	0.443727	0.443727	No
LAM	0.374149	0.373418	0.374149	Yes
MAX_vl	8.000000	8.000000	8.000000	Yes
MEAN_vl	2.305511	2.304642	2.305511	Yes
ENT_vl	0.709903	0.708647	0.709903	Yes

An R interface to Marwan’s commandline recurrence plots

IMPORTANT: Currently rp_cl can only run on an operating system that allows execution of 32-bit applications!

The crqa_cl() function is a wrapper for the commandline Recurrence Plots executable provided by Norbert Marwan.

The rp executable file is installed on your machine when the function rp_cl() is called for the first time:

It is renamed to rp from a platform specific file downloaded from the commandline Recurrence Plots site.
The file is copied to the directory: normalizePath("[path to casnet]/exec/",mustWork = FALSE)
- Make sure that you have rights to execute programs in this directory!
The latter location is stored as an option and can be read by calling getOption("casnet.path_to_rp")

If you cannot change the permissions on the folder where rp was downloaded, consider downloading the appropriate executable from the commandline Recurrence Plots site to a directory in which you have such permissions. Then change the path_to_rp option using options(casnet.path_to_rp="YOUR_PATH_TO_RP"). See the manual entry for rp_cl() for more details.

The platform specific rp command line executable files were created by Norbert Marwan and obtained under a Creative Commons License from the website of the Potsdam Institute for Climate Impact Research at: http://tocsy.pik-potsdam.de/

The full copyright statement on the website is as follows:

© 2004-2017 SOME RIGHTS RESERVED
University of Potsdam, Interdisciplinary Center for Dynamics of Complex Systems, Germany
Potsdam Institute for Climate Impact Research, Transdisciplinary Concepts and Methods, Germany
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 2.0 Germany License.

More information about recurrence quantification analysis can be found on the Recurrence Plot website.

Computational load: The Python solution [PyRQA]

When the time series you analyze are very long, the recurrence matrix will become very large and R will become very slow. One solution is to use R to run the Python program PyRQA or perhaps pyunicorn. The options for PyRQA are limited compared to the casnet functions, but the gain in processing speed is remarkable!

What follows is an example of how you could make PyRQA run in R using the package reticulate.

Setup the environment

Suppose you are on a machine that has both R and Python installed then the steps are:

Make sure Python and pip are up to date
Create a virtual (or a coda) environment.
Install PyRQA into the virtual environment.

You should only have to create and setup the environment once.

library(reticulate)

# OS requirements
# Python3.X is installed and updated.
# On MacOS you'll probably need to run these commands in a Terminal window:
python3 pip install --update pip # Updates the Python module installer
python3 pip intall pyrqa # Installs the pyrqa module on your machine

# First make sure you use the latest Python version
# You can check your machine by calling: reticulate::py_discover_config()
reticulate::use_python("/usr/local/bin/python3")

# Create a new environment "r-reticulate", the path is stored in vEnv
# On Windows use coda_create() see the reticulate manual.
vEnv <- reticulate::virtualenv_create("r-reticulate")

# Install pyrqa into the virtual environment
reticulate::virtualenv_install("r-reticulate","pyrqa")

# If you wish to remove the environment use: reticulate::virtualenv_remove("r-reticulate")

After the environment is set up:

Restart your R session and instruct the system to use Python in the virtual environment.
Import PyRQA into your R session.
Use the PyRQA functions that are now available as fields ($) of the imported object!

An important thing to note in the example below is the use of as.integer() to pass integer variables to Python.

# Make sure you associate reticulate with your virtual environment.
reticulate::use_virtualenv("r-reticulate", required = TRUE)

# Import pyrqa into your R session
pyrqa <- reticulate::import("pyrqa")

# Alternatively, you can import from a path in the virtual environment.
# On MacOS this will be a hidden folder in your home directory:
# '.virtualenvs/r-reticulate/lib/Python3.X/site-packages'
# pyrqa <- import_from_path(file.path(vEnv,"/lib/python3.9/site-packages"))

# Now perform RQA on your N = 10,000 time series!
Y <- cumsum(rnorm(10000))

# Automated parameter search will still take some time using casnet
system.time({
  emPar <- casnet::est_parameters(Y, doPlot = FALSE)
  emRad <- casnet::est_radius(y1 = Y, emLag = emPar$optimLag, emDim = emPar$optimDim)
  })
# user    system  elapsed 
# 299.732 89.094  393.620 

# About 5 minutes to find a delay, embedding dimension and radius yielding 5% recurrent points.

# Now do an RQA on the 10,000 x 10,000 matrix using Python
system.time({
time_series <- pyrqa$time_series$TimeSeries(Y, 
                                            embedding_dimension= as.integer(emPar$optimDim), 
                                            time_delay= as.integer(emPar$optimLag))
settings    <- pyrqa$settings$Settings(time_series, 
                                       analysis_type = pyrqa$analysis_type$Classic,
                                       neighbourhood = pyrqa$neighbourhood$FixedRadius(emRad$Radius),
                                       similarity_measure = pyrqa$metric$EuclideanMetric,
                                       theiler_corrector = 0)
computation <- pyrqa$computation$RQAComputation$create(settings)
result      <- computation$run()
})
# user   system  elapsed 
# 2.996  0.069   0.365 

# About 3 seconds for the analysis...
# That's really fast!

print(result)

RQA Result:
===========

Minimum diagonal line length (L_min): 2
Minimum vertical line length (V_min): 2
Minimum white vertical line length (W_min): 2

Recurrence rate (RR): 0.050090
Determinism (DET): 0.955821
Average diagonal line length (L): 10.634044
Longest diagonal line length (L_max): 9866
Divergence (DIV): 0.000101
Entropy diagonal lines (L_entr): 3.064460
Laminarity (LAM): 0.969709
Trapping time (TT): 14.930102
Longest vertical line length (V_max): 345
Entropy vertical lines (V_entr): 3.386939
Average white vertical line length (W): 265.518914
Longest white vertical line length (W_max): 9161
Longest white vertical line length inverse (W_div): 0.000109
Entropy white vertical lines (W_entr): 4.726210

Ratio determinism / recurrence rate (DET/RR): 19.081989
Ratio laminarity / determinism (LAM/DET): 1.014530

You can also save the Recurrence Plot.

RPcomputation <- pyrqa$computation$RPComputation$create(settings)
RPresult <- RPcomputation$run()
pyrqa$image_generator$ImageGenerator$save_recurrence_plot(RPresult$recurrence_matrix_reverse,'recurrence_plot_python.png')

knitr::include_graphics("recurrence_plot_python.png")

RP produced by PyRQA

Other options: Julia

The Julia software has a number of very powerful packages to simulate and analyze dynamical systems, see: https://juliadynamics.github.io/DynamicalSystems.jl/latest/

You can perform RQA (https://juliadynamics.github.io/DynamicalSystems.jl/latest/tutorial/#State-space-sets), but perhaps more interestingly, you can use a powerful automatic parameter selection algorithm for embedding called PECUZAL: https://juliadynamics.github.io/DelayEmbeddings.jl/stable/unified/

I use the freely available software Visual Studio Code to write and run Python (https://code.visualstudio.com/docs/languages/python) and Julia (https://code.visualstudio.com/docs/languages/julia)

Fred Hasselman

2024-11-20

RQA based on a matrix: `rp()`

Unordered categorical data

Continuous data

RQA based on massively parallel processing: `rqa_par()`

An R interface to Marwan’s commandline recurrence plots

Computational load: The Python solution [PyRQA]

Setup the environment

Other options: Julia

Recurrence Quantification Analysis

Fred Hasselman

2024-11-20

RQA based on a matrix: rp()

Unordered categorical data

Continuous data

RQA based on massively parallel processing: rqa_par()

An R interface to Marwan’s commandline recurrence plots

Computational load: The Python solution [PyRQA]

Setup the environment

Other options: Julia

RQA based on a matrix: `rp()`

RQA based on massively parallel processing: `rqa_par()`