Calculates the Recurrence Rate versus Recurrence Time power-law
Usage
rn_strengthDist(g, mode = c("in", "out", "all")[3], doPlot = TRUE)Examples
y <- rnorm(100)
RN <- rn(y, emLag=1, emDim=3, emRad=NA, weighted = TRUE, weightedBy = "rt", returnGraph = TRUE)
#> `emRad` was set to NA due to the value `weighted = TRUE`, if you want an unthresholded matrix set `weighted = FALSE`
rn_strengthDist(RN$g)
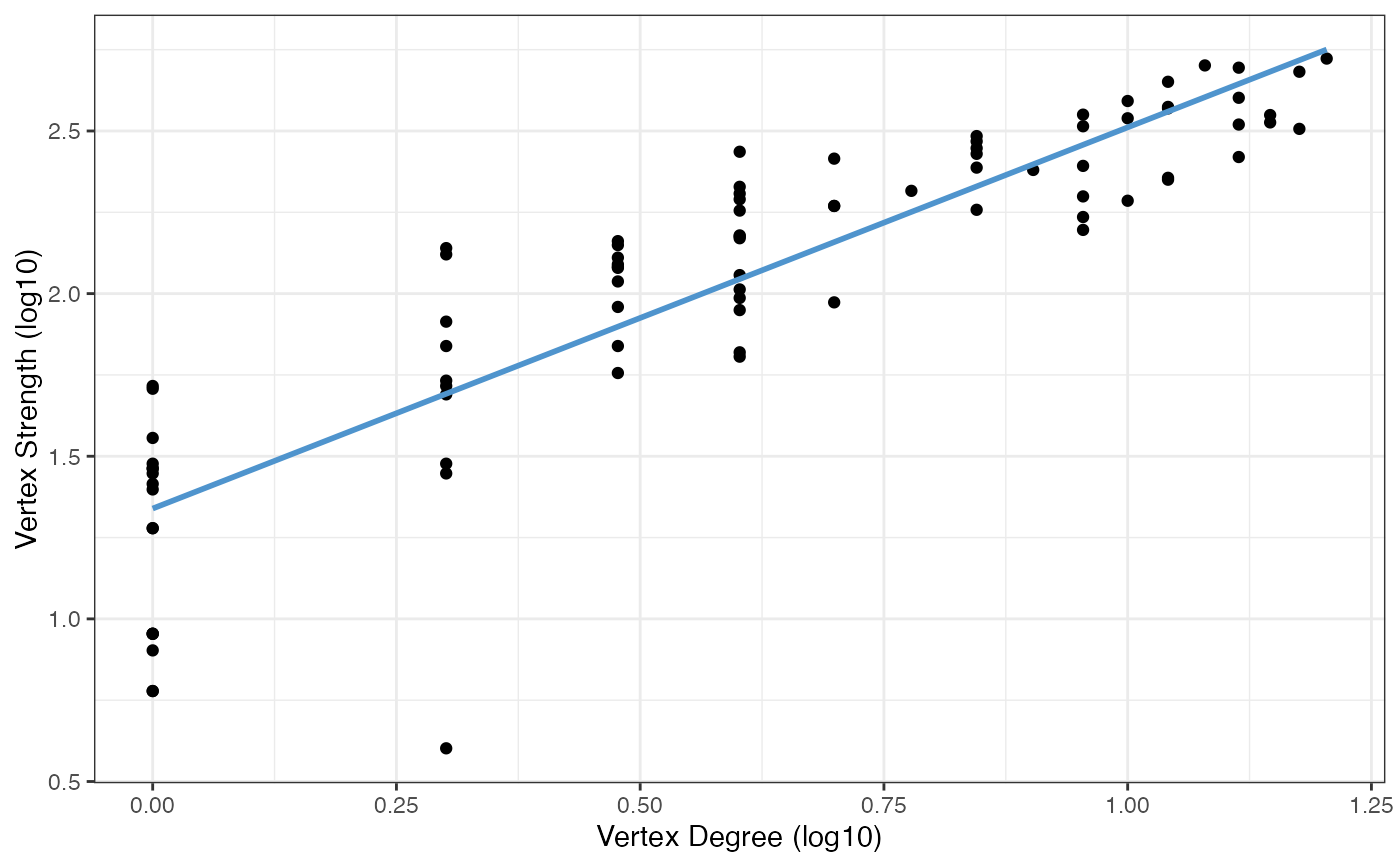#> xDegree yStrength xDegree_log10 yStrength_log10 PowerLaw PowerLawExponent
#> 1 11 674 1.0413927 2.8286599 2.553592 1.067562
#> 2 8 444 0.9030900 2.6473830 2.405945 1.067562
#> 3 8 404 0.9030900 2.6063814 2.405945 1.067562
#> 4 1 32 0.0000000 1.5051500 1.441840 1.067562
#> 5 1 6 0.0000000 0.7781513 1.441840 1.067562
#> 6 8 334 0.9030900 2.5237465 2.405945 1.067562
#> 7 4 167 0.6020600 2.2227165 2.084577 1.067562
#> 8 2 87 0.3010300 1.9395193 1.763209 1.067562
#> 9 2 78 0.3010300 1.8920946 1.763209 1.067562
#> 10 9 475 0.9542425 2.6766936 2.460554 1.067562
#> 11 7 275 0.8450980 2.4393327 2.344035 1.067562
#> 12 4 150 0.6020600 2.1760913 2.084577 1.067562
#> 13 1 75 0.0000000 1.8750613 1.441840 1.067562
#> 14 3 145 0.4771213 2.1613680 1.951197 1.067562
#> 15 4 212 0.6020600 2.3263359 2.084577 1.067562
#> 16 5 185 0.6989700 2.2671717 2.188035 1.067562
#> 17 3 123 0.4771213 2.0899051 1.951197 1.067562
#> 18 8 286 0.9030900 2.4563660 2.405945 1.067562
#> 19 2 51 0.3010300 1.7075702 1.763209 1.067562
#> 20 4 157 0.6020600 2.1958997 2.084577 1.067562
#> 21 6 215 0.7781513 2.3324385 2.272566 1.067562
#> 22 3 110 0.4771213 2.0413927 1.951197 1.067562
#> 23 5 157 0.6989700 2.1958997 2.188035 1.067562
#> 24 3 70 0.4771213 1.8450980 1.951197 1.067562
#> 25 6 187 0.7781513 2.2718416 2.272566 1.067562
#> 26 2 101 0.3010300 2.0043214 1.763209 1.067562
#> 27 11 369 1.0413927 2.5670264 2.553592 1.067562
#> 28 5 155 0.6989700 2.1903317 2.188035 1.067562
#> 29 9 219 0.9542425 2.3404441 2.460554 1.067562
#> 30 6 157 0.7781513 2.1958997 2.272566 1.067562
#> 31 9 293 0.9542425 2.4668676 2.460554 1.067562
#> 32 1 32 0.0000000 1.5051500 1.441840 1.067562
#> 33 2 35 0.3010300 1.5440680 1.763209 1.067562
#> 34 7 210 0.8450980 2.3222193 2.344035 1.067562
#> 35 1 25 0.0000000 1.3979400 1.441840 1.067562
#> 36 3 69 0.4771213 1.8388491 1.951197 1.067562
#> 37 3 69 0.4771213 1.8388491 1.951197 1.067562
#> 38 6 81 0.7781513 1.9084850 2.272566 1.067562
#> 39 8 214 0.9030900 2.3304138 2.405945 1.067562
#> 40 7 154 0.8450980 2.1875207 2.344035 1.067562
#> 41 4 52 0.6020600 1.7160033 2.084577 1.067562
#> 42 7 116 0.8450980 2.0644580 2.344035 1.067562
#> 43 10 296 1.0000000 2.4712917 2.509403 1.067562
#> 44 8 229 0.9030900 2.3598355 2.405945 1.067562
#> 45 4 62 0.6020600 1.7923917 2.084577 1.067562
#> 46 8 162 0.9030900 2.2095150 2.405945 1.067562
#> 47 4 102 0.6020600 2.0086002 2.084577 1.067562
#> 48 4 77 0.6020600 1.8864907 2.084577 1.067562
#> 49 5 137 0.6989700 2.1367206 2.188035 1.067562
#> 50 2 54 0.3010300 1.7323938 1.763209 1.067562
#> 51 8 265 0.9030900 2.4232459 2.405945 1.067562
#> 52 2 13 0.3010300 1.1139434 1.763209 1.067562
#> 53 6 81 0.7781513 1.9084850 2.272566 1.067562
#> 54 9 188 0.9542425 2.2741578 2.460554 1.067562
#> 55 8 220 0.9030900 2.3424227 2.405945 1.067562
#> 56 7 112 0.8450980 2.0492180 2.344035 1.067562
#> 57 8 109 0.9030900 2.0374265 2.405945 1.067562
#> 58 6 118 0.7781513 2.0718820 2.272566 1.067562
#> 59 1 25 0.0000000 1.3979400 1.441840 1.067562
#> 60 3 71 0.4771213 1.8512583 1.951197 1.067562
#> 61 9 188 0.9542425 2.2741578 2.460554 1.067562
#> 62 5 144 0.6989700 2.1583625 2.188035 1.067562
#> 63 6 163 0.7781513 2.2121876 2.272566 1.067562
#> 64 5 220 0.6989700 2.3424227 2.188035 1.067562
#> 65 5 90 0.6989700 1.9542425 2.188035 1.067562
#> 66 8 221 0.9030900 2.3443923 2.405945 1.067562
#> 67 4 177 0.6020600 2.2479733 2.084577 1.067562
#> 68 4 96 0.6020600 1.9822712 2.084577 1.067562
#> 69 6 187 0.7781513 2.2718416 2.272566 1.067562
#> 70 3 154 0.4771213 2.1875207 1.951197 1.067562
#> 71 3 94 0.4771213 1.9731279 1.951197 1.067562
#> 72 6 234 0.7781513 2.3692159 2.272566 1.067562
#> 73 8 316 0.9030900 2.4996871 2.405945 1.067562
#> 74 3 175 0.4771213 2.2430380 1.951197 1.067562
#> 75 3 121 0.4771213 2.0827854 1.951197 1.067562
#> 76 9 349 0.9542425 2.5428254 2.460554 1.067562
#> 77 8 396 0.9030900 2.5976952 2.405945 1.067562
#> 78 9 380 0.9542425 2.5797836 2.460554 1.067562
#> 79 5 184 0.6989700 2.2648178 2.188035 1.067562
#> 80 7 205 0.8450980 2.3117539 2.344035 1.067562
#> 81 6 283 0.7781513 2.4517864 2.272566 1.067562
#> 82 5 294 0.6989700 2.4683473 2.188035 1.067562
#> 83 5 232 0.6989700 2.3654880 2.188035 1.067562
#> 84 6 280 0.7781513 2.4471580 2.272566 1.067562
#> 85 8 314 0.9030900 2.4969296 2.405945 1.067562
#> 86 6 185 0.7781513 2.2671717 2.272566 1.067562
#> 87 7 285 0.8450980 2.4548449 2.344035 1.067562
#> 88 2 97 0.3010300 1.9867717 1.763209 1.067562
#> 89 3 171 0.4771213 2.2329961 1.951197 1.067562